विषयसूची:

वीडियो: किसी त्रिज्यखंड का क्षेत्रफल और त्रिज्या दिए जाने पर आप केंद्रीय कोण कैसे ज्ञात करते हैं?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2024-01-18 08:15
सेक्टर क्षेत्र से केंद्रीय कोण का निर्धारण
- (πr2) × ( केंद्रीय कोण डिग्री में 360 डिग्री) = क्षेत्र क्षेत्र . अगर केंद्रीय कोण रेडियन में मापा जाता है, इसके बजाय सूत्र बन जाता है:
- क्षेत्र क्षेत्र = आर2 × ( केंद्रीय कोण रेडियन में ÷ 2)।
- (θ 360 डिग्री) × r2.
- (52.3 100π) × 360।
- (52.3 ÷ 314) × 360.
इस प्रकार, आप त्रिज्या को देखते हुए केंद्रीय कोण कैसे ज्ञात करते हैं?
पाना NS मध्य कोण चाप की लंबाई से और RADIUS आप का भी उपयोग कर सकते हैं RADIUS वृत्त का और चाप की लंबाई to पाना NS केंद्रीय कोण . के माप को बुलाओ केंद्रीय कोण . तब: = s r, जहां s चाप की लंबाई है और r है RADIUS.
ऊपर के अलावा, आप किसी त्रिज्यखंड का केंद्रीय कोण कैसे ज्ञात करते हैं? केंद्रीय कोण का निर्धारण से क्षेत्र क्षेत्र दूसरे शब्दों में: (πr2) × ( केंद्रीय कोण डिग्री में 360 डिग्री) = क्षेत्र क्षेत्र। अगर केंद्रीय कोण रेडियन में मापा जाता है, सूत्र इसके बजाय बन जाता है: क्षेत्र क्षेत्र = आर2 × ( केंद्रीय कोण रेडियन में ÷ 2)।
ऊपर के अलावा, एक सेक्टर का क्षेत्रफल क्या है?
NS एक क्षेत्र का क्षेत्र एल के संदर्भ में कुल को गुणा करके प्राप्त किया जा सकता है क्षेत्र r2 एल के अनुपात से कुल परिधि 2πr।
परिधि का सूत्र क्या है?
a. की परिधि की गणना करने के लिए वृत्त , सूत्र C = πd का उपयोग करें, जहाँ "C" परिधि है, "d" व्यास है, और 3.14 है। यदि आपके पास व्यास के बजाय त्रिज्या है, तो व्यास प्राप्त करने के लिए इसे 2 से गुणा करें। आप a. की परिधि के लिए सूत्र का भी उपयोग कर सकते हैं वृत्त त्रिज्या का उपयोग करते हुए, जो C = 2πr है।
सिफारिश की:
आयतन दिए जाने पर आप लंबाई कैसे ज्ञात करते हैं?

माप की इकाइयाँ आयतन = लंबाई x चौड़ाई x ऊँचाई। घन का आयतन निकालने के लिए आपको केवल एक पक्ष जानने की जरूरत है। आयतन के लिए माप की इकाइयाँ घन इकाइयाँ हैं। वॉल्यूम तीन आयामों में है। आप किसी भी क्रम में पक्षों को गुणा कर सकते हैं। आप किस पक्ष को लंबाई, चौड़ाई या ऊंचाई कहते हैं, इससे कोई फर्क नहीं पड़ता
आप चाप की लंबाई और त्रिज्यखंड का क्षेत्रफल कैसे ज्ञात करते हैं?

एक केंद्रीय कोण, जो एक दीर्घ चाप द्वारा अंतरित किया जाता है, का माप 180° से बड़ा होता है। चाप लंबाई सूत्र का उपयोग किसी वृत्त के चाप की लंबाई ज्ञात करने के लिए किया जाता है; एल=आर&थीटा; एल = आर &थीटा;, जहां &थीटा; रेडियन में है। सेक्टर क्षेत्र पाया जाता है A=12θr2 A = 1 2 &थीटा; आर 2, जहां &थीटा; रेडियन में है
व्यास दिए जाने पर आप क्षेत्रफल कैसे ज्ञात करते हैं?

त्रिज्या वाले वृत्त का क्षेत्रफल ज्ञात करने के लिए, त्रिज्या का वर्ग करें, या इसे स्वयं से गुणा करें। फिर, वर्ग त्रिज्या को pi से गुणा करें, या 3.14, क्षेत्रफल प्राप्त करने के लिए। व्यास के साथ क्षेत्र को खोजने के लिए, बस व्यास को 2 से विभाजित करें, इसे त्रिज्या सूत्र में प्लग करें, और पहले की तरह हल करें
पृष्ठीय क्षेत्रफल दिए जाने पर आप किसी डिब्बे की ऊँचाई कैसे ज्ञात करते हैं?
एक बॉक्स के बारे में चीजें खोजें एक बॉक्स को अक्सर इसकी ऊंचाई, और इसकी चौड़ाई, डब्ल्यू, और इसकी लंबाई एल द्वारा विशेषता दी जाती है। बॉक्स की चौड़ाई, ऊंचाई और लंबाई सभी अलग-अलग हो सकती है। एक बॉक्स के अंदर आयतन, या स्थान की मात्रा h ×W × L है। एक बॉक्स का बाहरी सतह क्षेत्र 2(h ×W) + 2(h × L) + 2(W × L) है।
आप पाई चार्ट में किसी त्रिज्यखंड का कोण कैसे ज्ञात करते हैं?
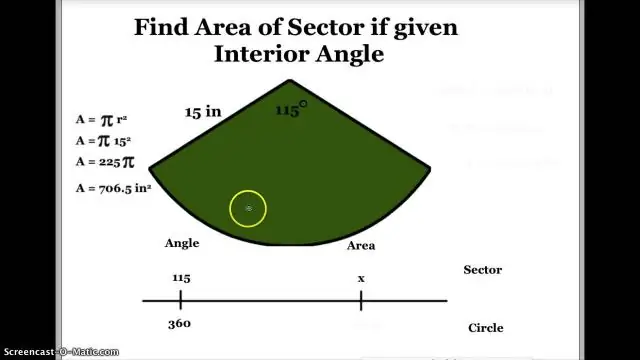
1 उत्तर किसी भी क्षेत्र में, विचार करने के लिए 3 भाग हैं: चाप की लंबाई परिधि का एक अंश है। ये क्षेत्र क्षेत्र पूरे क्षेत्र का एक अंश है। ये समकोण 360° का एक अंश है यदि त्रिज्यखंड पाई चार्ट का 20% है, तो इनमें से प्रत्येक भाग संपूर्ण का 20% है। 20%×360° 20100×360=72°
