
वीडियो: क्या किसी वृत्त की त्रिज्या शून्य हो सकती है?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
मेरी जानकारी के अनुसार, a. की परिभाषा में कुछ भी नहीं है वृत्त यह निर्दिष्ट करता है कि इसका RADIUS नहीं हो सकता शून्य … हालांकि, एक वृत्त साथ त्रिज्या शून्य के बहुत सारे गुण खो देता है हलकों . लेकिन एक वृत्त के साथ RADIUS का शून्य किसी अन्य के लिए बढ़ाया नहीं जा सकता RADIUS.
इसे ध्यान में रखते हुए, 0 त्रिज्या वाला एक वृत्त क्या है?
अगर RADIUS शून्य है, तो यह वास्तव में नहीं है वृत्त , लेकिन एक पतित कहा जा सकता है वृत्त --अर्थात, यदि आप a. की परिभाषा को थोड़ा आगे बढ़ाते हैं तो आपको क्या मिलता है वृत्त एक ही समीकरण का उपयोग करके लेकिन इसे बनाकर चरम पर ले जाकर RADIUS शून्य।
इसके बाद, प्रश्न यह है कि क्या एक वृत्त त्रिज्या से छोटा हो सकता है? हाँ एक सर्कल कैन कोई सकारात्मक है RADIUS . ए वृत्त के साथ RADIUS का से कम एक वर्ग की तरह ही समस्यारहित है, जिसकी भुजा की लंबाई से कम एक।
यह भी जानिए, क्या किसी वृत्त की त्रिज्या ऋणात्मक हो सकती है?
हां, त्रिज्या ऋणात्मक हो सकती है , जिसका अर्थ है कि यह उस के एक निर्दिष्ट पक्ष के बिल्कुल विपरीत दिशा में मापा जाता है वृत्त . अगर RADIUS शून्य है तो यह अधिक नहीं है a वृत्त लेकिन यह एक बिंदु है।
एक बिंदु वृत्त की त्रिज्या क्या है?
a. के लिए सामान्य समीकरण वृत्त x2+y2+2gx+2fy+c=0 है, जहां h=−g और k=−f. NS RADIUS तब r=√g2+f2−c है। अगर g2+f2−c=0, तो यह a. है बिंदु वृत्त . अगर g2+f2−c>0, तो यह वास्तविक है वृत्त.
सिफारिश की:
पाई का उपयोग करके आप किसी वृत्त की त्रिज्या कैसे ज्ञात करते हैं?
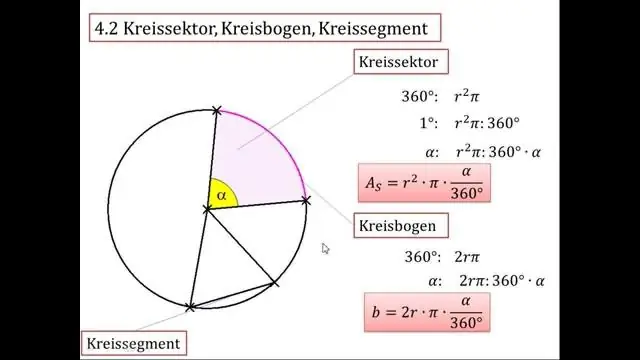
परिधि का उपयोग करके एक वृत्त की त्रिज्या की गणना करने के लिए, वृत्त की परिधि लें और इसे 2 गुना π से विभाजित करें। 15 की परिधि वाले एक वृत्त के लिए, आप 15 को 2 गुणा 3.14 से विभाजित करेंगे और दशमलव बिंदु को लगभग 2.39 के अपने उत्तर में गोल करेंगे।
यदि किसी कोशिका में राइबोसोम काम नहीं कर रहे हों तो सबसे अधिक संभावना क्या होगी?

राइबोसोम ऐसे अंग हैं जो प्रोटीन बनाते हैं। कोशिकाएँ प्रोटीन का उपयोग महत्वपूर्ण कार्य करने के लिए करती हैं जैसे सेलुलर क्षति की मरम्मत और रासायनिक प्रक्रियाओं को निर्देशित करना। इन राइबोसोम के बिना, कोशिकाएं प्रोटीन का उत्पादन नहीं कर पाएंगी और ठीक से काम नहीं कर पाएंगी
त्रिज्या और वक्रता त्रिज्या में क्या अंतर है?

वक्रता त्रिज्या वृत्त की त्रिज्या है जो किसी दिए गए बिंदु पर वक्र को स्पर्श करती है और उस बिंदु पर समान स्पर्शरेखा और वक्रता होती है। त्रिज्या वृत्त की परिधि या गोले की सतह पर केंद्र और किसी अन्य बिंदु के बीच की दूरी है। मंडलियों में आपको त्रिज्या शब्द का प्रयोग करना चाहिए
आप किसी वृत्त के वर्ग की त्रिज्या कैसे ज्ञात करते हैं?

त्रिज्या वाले वृत्त का क्षेत्रफल ज्ञात करने के लिए, त्रिज्या का वर्ग करें या इसे स्वयं से गुणा करें। फिर, क्षेत्रफल प्राप्त करने के लिए वर्ग त्रिज्या को pi, या 3.14 से गुणा करें। व्यास के साथ क्षेत्र को खोजने के लिए, बस व्यास को 2 से विभाजित करें, इसे त्रिज्या सूत्र में प्लग करें, और पहले की तरह हल करें
5 त्रिज्या वाले वृत्त का समीकरण क्या है?

एक वृत्त का मानक रूप नीचे दिया गया है: (x - h)2 + (y - k)2 = r2, जहां केंद्र (h, k) पर स्थित है और r त्रिज्या की लंबाई है। इस स्थिति में, h -3 होगा, k 6 होगा, और r 5 . होगा
