वीडियो: पाई का उपयोग करके आप किसी वृत्त की त्रिज्या कैसे ज्ञात करते हैं?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
गणना करने के लिए एक वृत्त की त्रिज्या द्वारा का उपयोग करते हुए परिधि, की परिधि ले लो वृत्त और इसे 2 गुना से भाग दें मैं . एक के लिए सर्कल के साथ 15 की परिधि में, आप 15 को 2 गुणा 3.14 से विभाजित करेंगे और दशमलव बिंदु को लगभग 2.39 के अपने उत्तर में गोल करेंगे।
इस संबंध में त्रिज्या ज्ञात करने का सूत्र क्या है?
दो सूत्रों जो खोजने के लिए उपयोगी हैं RADIUS एक वृत्त के C=2*pi*r और A=pi*r^2 हैं। हम अपने चर r को हल करने में बीजगणित कौशल का उपयोग करते हैं। हम जानते हैं कि अचर pi हमेशा 3.14 होता है। से संबंधित एक और शब्द RADIUS व्यास है, जो हमेशा दो गुना होता है RADIUS.
इसके अलावा, एक वृत्त कैलकुलेटर की त्रिज्या क्या है? इस मान को परिधि के सूत्र में रखें: C = 2 * * R = 2 * π * 14 = 87.9646 सेमी। आप इसका उपयोग a. का क्षेत्रफल ज्ञात करने के लिए भी कर सकते हैं वृत्त : ए = π * आर² = π * 14² = 615.752 सेमी²। अंत में, आप व्यास पा सकते हैं - यह केवल दोगुना है RADIUS : डी = 2 * आर = 2 * 14 = 28 सेमी।
इसी तरह, एक वृत्त की त्रिज्या क्या है?
NS एक वृत्त की त्रिज्या के केंद्र से दूरी है वृत्त इसकी परिधि के किसी भी बिंदु पर। [1] खोजने का सबसे आसान तरीका RADIUS व्यास को आधे में विभाजित करके है।
आप त्रिभुज का क्षेत्रफल कैसे ज्ञात करते हैं?
प्रति पाना NS क्षेत्र का त्रिकोण , आधार को ऊंचाई से गुणा करें, और फिर 2 से विभाजित करें। 2 से विभाजन इस तथ्य से आता है कि एक समांतर चतुर्भुज को 2 में विभाजित किया जा सकता है। त्रिभुज . उदाहरण के लिए, बाईं ओर के आरेख में, क्षेत्र प्रत्येक की त्रिकोण डेढ़ के बराबर है क्षेत्र समांतर चतुर्भुज का।
सिफारिश की:
किसी त्रिज्यखंड का क्षेत्रफल और त्रिज्या दिए जाने पर आप केंद्रीय कोण कैसे ज्ञात करते हैं?

सेक्टर क्षेत्र से केंद्रीय कोण का निर्धारण (πr2) × (केंद्रीय कोण डिग्री ÷ 360 डिग्री में) = सेक्टर क्षेत्र। यदि केंद्रीय कोण को रेडियन में मापा जाता है, तो इसके बजाय सूत्र बन जाता है: त्रिज्यखंड क्षेत्र = r2 × (रेडियन ÷ 2 में केंद्रीय कोण)। (θ 360 डिग्री) × r2. (52.3 100π) × 360. (52.3 ÷ 314) × 360
अनुभवजन्य नियम का उपयोग करके आप अनुमानित प्रतिशत कैसे ज्ञात करते हैं?

वक्र के नीचे का क्षेत्रफल x = 9 से x = 13 तक ज्ञात करना। अनुभवजन्य नियम या 68-95-99.7% नियम डेटा का अनुमानित प्रतिशत देता है जो एक मानक विचलन (68%), दो मानक विचलन (95%) के अंतर्गत आता है। , और माध्य के तीन मानक विचलन (99.7%)
आप किसी वृत्त के वर्ग की त्रिज्या कैसे ज्ञात करते हैं?

त्रिज्या वाले वृत्त का क्षेत्रफल ज्ञात करने के लिए, त्रिज्या का वर्ग करें या इसे स्वयं से गुणा करें। फिर, क्षेत्रफल प्राप्त करने के लिए वर्ग त्रिज्या को pi, या 3.14 से गुणा करें। व्यास के साथ क्षेत्र को खोजने के लिए, बस व्यास को 2 से विभाजित करें, इसे त्रिज्या सूत्र में प्लग करें, और पहले की तरह हल करें
अवोगाद्रो के नियम का उपयोग करके आप आयतन कैसे ज्ञात करते हैं?

अवोगाद्रो का नियम बताता है कि गैस के मोलों की संख्या और उसके आयतन के बीच सीधा संबंध होता है। इसे समीकरण का उपयोग करके भी दिखाया जा सकता है: V1/n1 = V2/n2। यदि मोलों की संख्या दोगुनी कर दी जाए, तो आयतन दोगुना हो जाएगा
आप पाई चार्ट में किसी त्रिज्यखंड का कोण कैसे ज्ञात करते हैं?
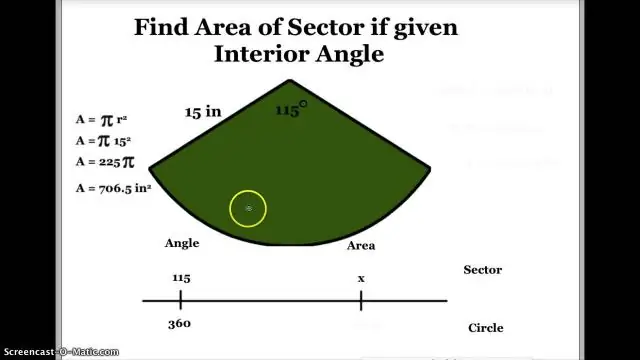
1 उत्तर किसी भी क्षेत्र में, विचार करने के लिए 3 भाग हैं: चाप की लंबाई परिधि का एक अंश है। ये क्षेत्र क्षेत्र पूरे क्षेत्र का एक अंश है। ये समकोण 360° का एक अंश है यदि त्रिज्यखंड पाई चार्ट का 20% है, तो इनमें से प्रत्येक भाग संपूर्ण का 20% है। 20%×360° 20100×360=72°
