विषयसूची:

वीडियो: आप दो त्रिभुजों के लिए कैसे हल करते हैं?
2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
SSA त्रिभुजों को हल करना
- दूसरे में से किसी एक की गणना करने के लिए पहले द लॉ ऑफ़ साइन्स का उपयोग करें दो कोण;
- फिर तीन कोणों का प्रयोग करके 180° का योग दूसरे कोण को खोजने के लिए करें कोण ;
- अंत में अज्ञात पक्ष को खोजने के लिए फिर से द लॉ ऑफ साइन्स का उपयोग करें।
बस इतना ही, आप त्रिभुज का दूसरा हल कैसे निकालते हैं?
यह निर्धारित करने के लिए कि दूसरा वैध कोण है या नहीं:
- देखें कि क्या आपको दो भुजाएँ दी गई हैं और कोण (SSA) के बीच में नहीं है।
- अज्ञात कोण का मान ज्ञात कीजिए।
- एक बार जब आप अपने कोण का मान प्राप्त कर लेते हैं, तो संभावित दूसरे कोण को खोजने के लिए इसे 180° से घटाएं।
- नए कोण को मूल कोण में जोड़ें।
इसके अतिरिक्त, आप त्रिभुज का क्षेत्रफल कैसे ज्ञात करते हैं? प्रति पाना NS क्षेत्र का त्रिकोण , आधार को ऊंचाई से गुणा करें, और फिर 2 से विभाजित करें। 2 से विभाजन इस तथ्य से आता है कि एक समांतर चतुर्भुज को 2 में विभाजित किया जा सकता है। त्रिभुज . उदाहरण के लिए, बाईं ओर के आरेख में, क्षेत्र प्रत्येक की त्रिकोण डेढ़ के बराबर है क्षेत्र समांतर चतुर्भुज का।
इस संबंध में, हीरोन का क्षेत्रफल सूत्र क्या है?
ज्यामिति में, हीरोन का सूत्र (कभी-कभी Hero's. कहा जाता है) सूत्र ), अलेक्जेंड्रिया के हीरो के नाम पर, देता है क्षेत्र एक त्रिभुज का, जब तीनों भुजाओं की लंबाई ज्ञात हो। अन्य त्रिभुज के विपरीत क्षेत्र सूत्र, पहले त्रिभुज में कोणों या अन्य दूरियों की गणना करने की आवश्यकता नहीं है।
Cpctc का क्या अर्थ है?
सर्वांगसम त्रिभुजों के संगत भाग सर्वांगसम होते हैं
सिफारिश की:
परमाणु इलेक्ट्रॉन कैसे प्राप्त करते हैं और कैसे खोते हैं?

आयनिक बंध। हमारी क्रूड, वैचारिक परिभाषा के अनुसार, रासायनिक बंधन या तो परमाणुओं के बीच इलेक्ट्रॉन हस्तांतरण या इलेक्ट्रॉनों के बंटवारे से बन सकते हैं। जब परमाणु इलेक्ट्रॉन खो देते हैं या प्राप्त कर लेते हैं, तो वे आयन कहलाते हैं। इलेक्ट्रॉनों की हानि एक परमाणु को शुद्ध धनात्मक आवेश के साथ छोड़ देती है, और परमाणु को धनायन कहा जाता है
क्या कोज्या नियम सभी त्रिभुजों के लिए कार्य करता है?

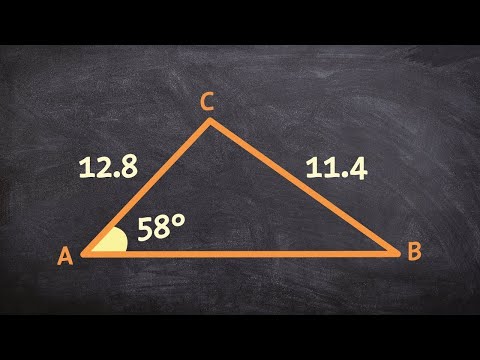
उस से, आप तीसरे पक्ष को खोजने के लिए कोसाइन के नियम का उपयोग कर सकते हैं। यह किसी भी त्रिभुज पर काम करता है, न कि केवल समकोण त्रिभुज पर। जहाँ a और b दो दी गई भुजाएँ हैं, C उनका सम्मिलित कोण है, और c अज्ञात तीसरी भुजा है
आप त्रिभुजों को कैसे हल करते हैं?

आपके हल करने वाले टूलबॉक्स में (आपकी कलम, कागज़ और कैलकुलेटर के साथ) आपके पास ये 3 समीकरण हैं: कोण हमेशा 180° जोड़ते हैं: A + B + C = 180° ज्या का नियम (साइन नियम): जब कोई कोण होता है एक पक्ष के विपरीत, यह समीकरण बचाव के लिए आता है। कोसाइन का नियम (कोसाइन नियम):
आप SAS समरूपता अभिगृहीत भुजा कोण भुजा का उपयोग करके 2 त्रिभुजों को समरूप कैसे सिद्ध कर सकते हैं?

SAS समानता प्रमेय में कहा गया है कि यदि एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हों और दोनों में सम्मिलित कोण सर्वांगसम हों, तो दोनों त्रिभुज समरूप होते हैं। एक समानता परिवर्तन एक या एक से अधिक कठोर परिवर्तन है जिसके बाद फैलाव होता है
आप गुणा को कैसे पार करते हैं और भिन्नों की तुलना कैसे करते हैं?

दो भिन्नों को क्रॉस-गुणा करने के लिए: पहले भिन्न के अंश को दूसरे भिन्न के हर से गुणा करें और उत्तर को संक्षेप में लिखें। दूसरे भिन्न के अंश को पहले भिन्न के हर से गुणा करें और उत्तर को संक्षेप में लिखें
