
वीडियो: त्वरण का समाकल क्या दर्शाता है?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
त्वरण है समय के संबंध में विस्थापन का दूसरा व्युत्पन्न, या समय के संबंध में वेग का पहला व्युत्पन्न: उलटा प्रक्रिया: एकीकरण . वेग है एक त्वरण का अभिन्न अंग अधिक समय तक। विस्थापन है एक अभिन्न समय के साथ वेग का।
इसे ध्यान में रखते हुए, जब आप त्वरण को एकीकृत करते हैं तो क्या होता है?
परिभाषा से, त्वरण समय के संबंध में वेग का पहला व्युत्पन्न है। खोजने के लिए वेग में अंतर करने के बजाय त्वरण , त्वरण को एकीकृत करें वेग खोजने के लिए। यह हमें वेग-समय समीकरण देता है। अगर हम मान लीजिए त्वरण स्थिर है, हम गति का तथाकथित पहला समीकरण प्राप्त करें [1]।
दूसरे, यदि आप विस्थापन को एकीकृत करते हैं तो क्या होगा? प्रत्यक्ष गणितीय अर्थ में, अभिन्न का विस्थापन समय के संबंध में बस एक स्थिरांक है एकीकरण . अगर तुम के परिवर्तन की दर के रूप में वेग के बारे में सोचो विस्थापन , आप ऐसा कर सकते हैं सोच विस्थापन एक बिंदु के परिवर्तन की दर के रूप में, इसलिए अभिन्न का विस्थापन सिर्फ एक बिंदु होगा।
इसी प्रकार कोई यह पूछ सकता है कि स्थिति का समाकलन क्या दर्शाता है?
NS स्थिति का अभिन्न अंग एक अक्ष के साथ w.r.t दूसरी धुरी आपको वक्र के उस खंड और x-अक्ष द्वारा मैप किया गया क्षेत्र देता है। NS स्थिति का अभिन्न अंग समय के संबंध में आपको "मीटर सेकंड" इकाइयों के साथ एक मात्रा देता है।
त्वरण का सूत्र क्या है?
त्वरण (ए) समय में परिवर्तन (Δt) पर वेग (Δv) में परिवर्तन है, जिसे द्वारा दर्शाया गया है समीकरण ए = v/Δt. यह आपको मापने की अनुमति देता है कि मीटर प्रति सेकंड वर्ग (एम/एस ^ 2) में कितनी तेजी से वेग बदलता है। त्वरण एक सदिश राशि भी है, इसलिए इसमें परिमाण और दिशा दोनों शामिल हैं।
सिफारिश की:
आप कोणीय वेग और त्वरण कैसे ज्ञात करते हैं?
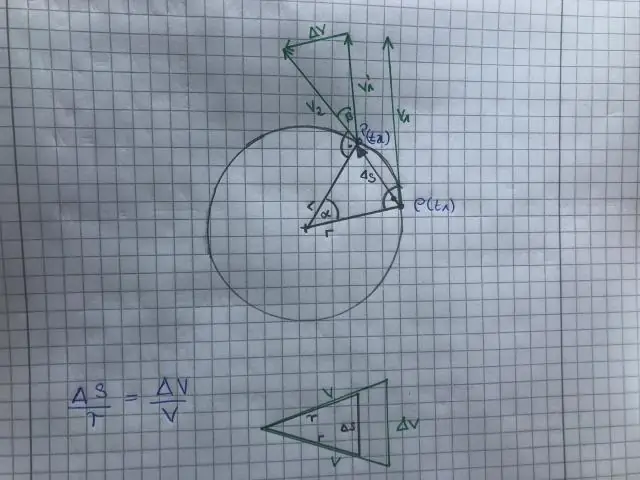
समीकरण रूप में, कोणीय त्वरण निम्नानुसार व्यक्त किया जाता है: α=ΔωΔt α = Δ और ओमेगा; &डेल्टा; टी, जहां &डेल्टा;ω कोणीय वेग में परिवर्तन है और Δt समय में परिवर्तन है। कोणीय त्वरण की इकाइयाँ हैं (rad/s)/s, या rad/s2
आप वेग को त्वरण ग्राफ में कैसे बदलते हैं?
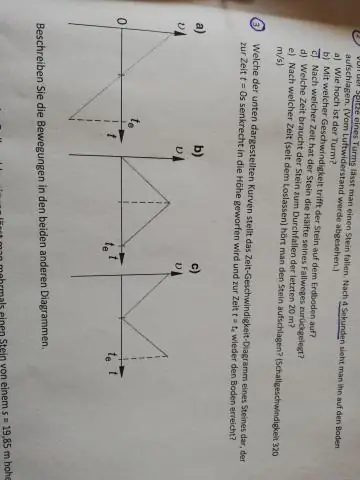
यदि ग्राफ वेग बनाम समय है, तो क्षेत्रफल ज्ञात करना आपको विस्थापन देगा, क्योंकि वेग = विस्थापन/समय। यदि ग्राफ त्वरण बनाम समय है, तो क्षेत्रफल ज्ञात करने से आपको वेग में परिवर्तन प्राप्त होता है, क्योंकि त्वरण = वेग/समय में परिवर्तन
आप वेग और त्वरण को कैसे रेखांकन करते हैं?

सिद्धांत यह है कि वेग-समय ग्राफ पर रेखा का ढलान वस्तु के त्वरण के बारे में उपयोगी जानकारी प्रकट करता है। यदि त्वरण शून्य है, तो ढाल शून्य है (अर्थात एक क्षैतिज रेखा)। यदि त्वरण धनात्मक है, तो ढाल धनात्मक है (अर्थात ऊपर की ओर झुकी हुई रेखा)
अभिकेन्द्र त्वरण के लिए आप कैसे हल करते हैं?

केन्द्रक ('केंद्र-मांग') त्वरण एक वृत्त के केंद्र की ओर अंदर की ओर गति है। त्वरण वेग के वर्ग के बराबर होता है, जिसे वृत्ताकार पथ की त्रिज्या से विभाजित किया जाता है
जब आप किसी गेंद को सीधे ऊपर की ओर फेंकते हैं तो उसके त्वरण के बारे में क्या सत्य है?

आपने गेंद को सीधे ऊपर फेंका, इसलिए ऊपर की ओर जाने पर उसकी दिशा ऊपर की ओर बनी रहती है। हालांकि, गेंद धीमी हो जाती है, इसलिए इसकी गति कम हो जाती है। गेंद की गति के शीर्ष पर, इसकी गति शून्य होती है। गेंद की गति के शीर्ष पर, यह अभी भी गुरुत्वाकर्षण से प्रभावित है, इसलिए इसमें अभी भी गुरुत्वाकर्षण के कारण त्वरण है: 9.8 m/s2
