विषयसूची:
वीडियो: अवर्गीकृत आँकड़ों के लिए केन्द्रीय प्रवृत्ति के माप क्या हैं?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
शब्द केंद्रीय प्रवृत्ति के एक सेट के मध्य, या विशिष्ट, मान को संदर्भित करता है आंकड़े , जो सबसे अधिक है मापा तीन मीटर का उपयोग करके: माध्य, माध्यिका और बहुलक। माध्य, माध्यिका और बहुलक को के रूप में जाना जाता है केंद्रीय प्रवृत्ति के उपाय.
इस प्रकार, समूहीकृत आँकड़ों के लिए केन्द्रीय प्रवृत्ति का माप क्या है?
मध्यमान मध्यम मोड: केंद्रीय प्रवृत्ति के उपाय . मीन मीन फॉर समूहीकृत डेटा समूहीकृत डेटा क्या हैं आंकड़े या अंक जिन्हें बारंबारता बंटन में व्यवस्थित किया जाता है।
इसी प्रकार, आप अवर्गीकृत आँकड़ों के माध्य को कैसे हल करते हैं? कदम
- अपना डेटा एकत्र करें और गिनें। डेटा मानों के किसी भी सेट के लिए, माध्य केंद्रीय मान का एक माप है।
- डेटा मानों का योग ज्ञात कीजिए। माध्य ज्ञात करने का पहला चरण सभी डेटा बिंदुओं के योग की गणना करना है।
- माध्य ज्ञात करने के लिए विभाजित करें। अंत में, योग को मानों की संख्या से विभाजित करें।
इसके अलावा, अवर्गीकृत आँकड़ों के लिए माध्य माध्यिका और बहुलक ज्ञात करने के लिए किस सूत्र का प्रयोग किया जाता है?
सारांश
- समूहीकृत आंकड़ों के लिए, हम सटीक माध्य, माध्यिका और बहुलक नहीं खोज सकते, हम केवल अनुमान दे सकते हैं।
- माध्य का अनुमान लगाने के लिए वर्ग अंतराल के मध्य बिंदुओं का उपयोग करें: अनुमानित माध्य = (मध्य बिंदु × आवृत्ति) आवृत्ति का योग।
- माध्यिका उपयोग का अनुमान लगाने के लिए: अनुमानित माध्यिका = L + (n/2) - BG × w।
- मोड उपयोग का अनुमान लगाने के लिए:
समूहीकृत आँकड़ों के लिए बहुलक का सूत्र क्या है?
हमारे शिक्षक कहते हैं a सूत्र पता लगाने के लिए तरीका , वह है Z=L1+(F1-F0)/(2F1-F0-F2)*i जहां: L1 = मोडल क्लास F1 की निचली सीमा = मोडल क्लास फ़्रीक्वेंसी। F2 = बहुलक वर्ग आवृत्ति के ठीक बाद। F0 = बहुलक वर्ग आवृत्ति से ठीक पहले।
सिफारिश की:
लंबाई के लिए अंग्रेजी प्रणाली माप क्या है?

लंबाई क्षेत्र 12 इंच = 1 फुट 144 वर्ग इंच 3 फीट = 1 गज 9 वर्ग फुट 220 गज = 1 फर्लांग 4,840 वर्ग गज 8 फर्लांग = 1 मील 640 एकड़
आँकड़ों में माप के पैमाने क्या हैं?

मापन पैमानों का उपयोग चरों को वर्गीकृत और/या परिमाणित करने के लिए किया जाता है। यह पाठ माप के चार पैमानों का वर्णन करता है जो आमतौर पर सांख्यिकीय विश्लेषण में उपयोग किए जाते हैं: नाममात्र, क्रमिक, अंतराल और अनुपात पैमाने
सांख्यिकी में अवर्गीकृत डेटा क्या है?
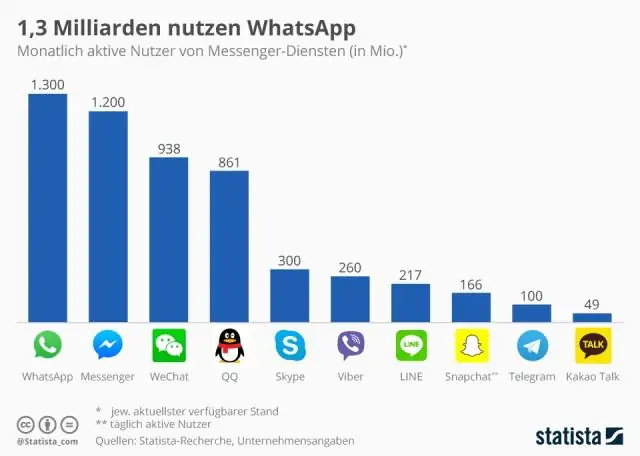
असमूहीकृत डेटा वह डेटा है जिसे आप पहली बार किसी प्रयोग या अध्ययन से एकत्र करते हैं। डेटा कच्चा है - यानी, इसे श्रेणियों, वर्गीकृत, या अन्यथा समूहीकृत नहीं किया जाता है। डेटा का एक असमूहीकृत सेट मूल रूप से संख्याओं की एक सूची है
ऊंचाई के लिए माप का स्तर क्या है?

व्यक्तियों और वस्तुओं की भौतिक विशेषताओं को अनुपात तराजू से मापा जा सकता है, और इस प्रकार, ऊंचाई और वजन अनुपात माप के उदाहरण हैं। 0 के स्कोर का मतलब है कि ऊंचाई या वजन का पूर्ण अभाव है। एक व्यक्ति जो 1.2 मीटर (4 फीट) लंबा है, वह 1.8-मीटर- (6-फुट-) लंबे व्यक्ति के रूप में दो-तिहाई लंबा है
एक समूह में ऊपर से नीचे तक परमाणु आकार के लिए आवर्त प्रवृत्ति क्या है?
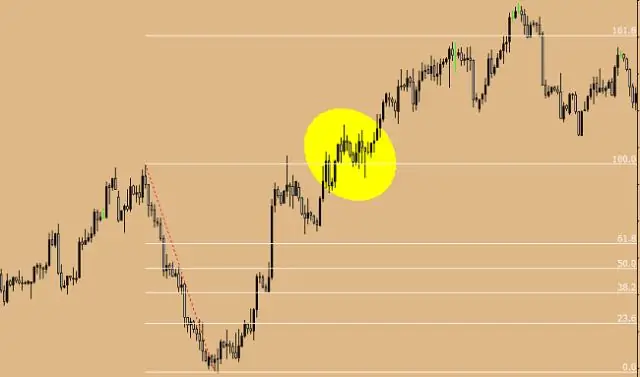
एक समूह में ऊपर से नीचे की ओर, इलेक्ट्रोनगेटिविटी कम हो जाती है। इसका कारण यह है कि परमाणु क्रमांक एक समूह में नीचे की ओर बढ़ता है, और इस प्रकार वैलेंस इलेक्ट्रॉनों और नाभिक, या एक अधिक परमाणु त्रिज्या के बीच एक बढ़ी हुई दूरी होती है
