क्या ची वर्ग ऋणात्मक हो सकता है?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36

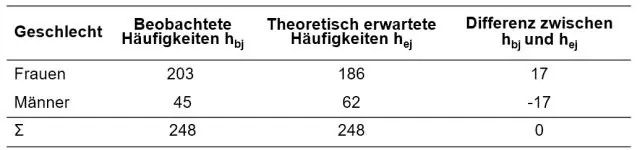
करना तुम्हारा मतलब है: कर सकना के मान ची स्क्वायर कभी भी नकारात्मक ? जवाब न है। ए. का मान ची स्क्वायर नहीं हो सकता नकारात्मक क्योंकि यह के योग पर आधारित है वर्ग अंतर (प्राप्त और अपेक्षित परिणामों के बीच)।

इसी तरह, काई वर्ग वितरण हमेशा सकारात्मक क्यों होता है?

की गणना मूल्य ची - वर्ग है हमेशा सकारात्मक क्योंकि प्रेक्षित आवृत्ति और अपेक्षित आवृत्ति के बीच का अंतर है वर्ग , वह है (ओ - ई)² और डिमोनेटर अपेक्षित संख्या है जो भी होनी चाहिए सकारात्मक . NS ची - वर्ग वितरण सकारात्मक रूप से तिरछा है।

ऊपर के अलावा, क्या ची वर्ग 0 हो सकता है? आंकड़ों में, गैर-केंद्रीय ची - वर्ग के साथ वितरण शून्य स्वतंत्रता की कोटियां कर सकते हैं शून्य परिकल्पना के परीक्षण में उपयोग किया जा सकता है कि एक नमूना अंतराल पर एक समान वितरण से है ( 0 , 1) । यह तुच्छ है कि एक "केंद्रीय" ची -वर्ग वितरण. के साथ शून्य स्वतंत्रता की डिग्री सभी संभावनाओं को केंद्रित करती है शून्य.

इसी तरह, क्या आपके पास नकारात्मक T मान हो सकता है?

यदि यह परिकल्पित से छोटा है मूल्य , फिर टी -सांख्यिकी नकारात्मक होगा . यदि यह बड़ा है, तो टी -सांख्यिकी होगा सकारात्मक। ए नकारात्मक संकेत का तात्पर्य है कि नमूना माध्य परिकल्पित माध्य से कम है।

आप शून्य परिकल्पना ची स्क्वायर को कैसे अस्वीकार करते हैं?

दूसरे शब्दों में, जब परिकलित x² आँकड़ा 0.05 प्रायिकता स्तर के लिए तालिका में महत्वपूर्ण मान से अधिक है, तो हम कर सकते हैं शून्य परिकल्पना को अस्वीकार करें समान वितरण के।