
वीडियो: क्या आप गैर समकोण त्रिभुजों पर sin और cos का उपयोग कर सकते हैं?
2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
दूसरे पर विचार करें गैर - सही त्रिकोण , लेबल किया गया है जैसा कि पक्ष लंबाई x और y के साथ दिखाया गया है। वे कैन एक उपयोगी कानून प्राप्त करें जिसमें केवल कोज्या समारोह। कोसाइन का नियम कर सकते हैं कोण या भुजा की माप ज्ञात करने के लिए उपयोग किया जाता है गैर - सही त्रिकोण अगर हम जानिए: तीन भुजाएँ और कोई कोण नहीं।
इसके बाद, कोई यह भी पूछ सकता है कि क्या एक गैर समकोण त्रिभुज पर ज्या का प्रयोग किया जा सकता है?
का कानून सीन्स कर सकते हैं होना उपयोग किया गया तिरछा हल करने के लिए त्रिभुज , जो हैं गैर - समकोण त्रिभुज . के कानून के अनुसार साइनेस , कोणों में से एक के माप का अनुपात इसके विपरीत पक्ष की लंबाई के अन्य दो अनुपातों के बराबर होता है कोण विपरीत दिशा में मापें। तीन संभावित मामले हैं: एएसए, एएएस, एसएसए।
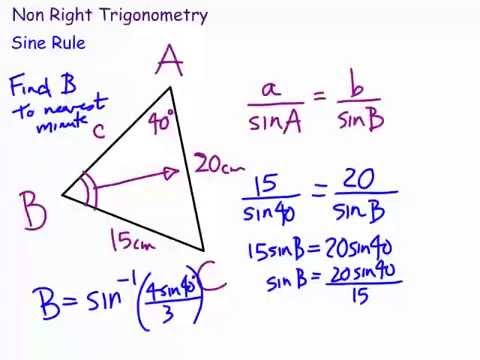
दूसरे, क्या आप गैर समकोण त्रिभुजों पर सोहकाहटो कर सकते हैं? कैसे त्रिकोणमिति पर इस्तेमाल किया गया गैर - अधिकार कोणीय त्रिभुज ? प्रति करना यह वहाँ हैं दो नियम, साइन नियम और कोसाइन नियम। साइन नियम a/Sin A = b/Sin B = c/Sin C है। साइन नियम का उपयोग तब किया जाता है जब आप या तो दो कोणों के vlaue हैं और एक पक्ष, या दो पक्ष और एक विपरीत कोण एक a. के उन पक्षों में से त्रिकोण.
इसके अलावा, क्या कोज्या अनुपात गैर समकोण त्रिभुजों के साथ कार्य करता है?
त्रिकोणमितीय कार्यों को परिभाषित किया गया है a सही त्रिकोण , लेकिन इसका मतलब यह नहीं है कि वे केवल काम के लिये समकोण त्रिभुज ! उदाहरण के लिए, ऐसे कानून हैं जो काम के लिये गैर - समकोण त्रिभुज . इन्हें ज्या के नियम और के नियम के रूप में जाना जाता है कोसाइन . सी^2 = ए^2 + बी^2 क्योंकि कोज्या 90 डिग्री 0 है।
त्रिभुज के लिए ज्या नियम क्या है?
NS साइन नियम साइन्स का कानून ( साइन नियम ) एक महत्वपूर्ण. है नियम किसी की भुजाओं और कोणों से संबंधित त्रिकोण (इसका समकोण होना आवश्यक नहीं है!): यदि a, b और c कोणों A, B और C के विपरीत भुजाओं की लंबाई हैं। त्रिकोण , तो: ए = बी = सी। सीना पाप बी पाप सी।
सिफारिश की:
क्या एक आयत में चार समकोण होते हैं?

एक आयत में विपरीत भुजाओं के दो जोड़े समानांतर और चार समकोण होते हैं। यह एक समांतर चतुर्भुज भी है, क्योंकि इसमें समानांतर भुजाओं के दो जोड़े हैं। एक वर्ग में समानांतर भुजाओं के दो जोड़े, चार समकोण होते हैं और चारों भुजाएँ बराबर होती हैं। नहीं, क्योंकि समचतुर्भुज में 4 समकोण होने की आवश्यकता नहीं होती है
गैर-ध्रुवीय बंधों वाले एक गैर-ध्रुवीय अणु का सूत्र कौन सा है?

(1), (3) H2O और NH3 ऐसे अणु हैं जिनमें ध्रुवीय सहसंयोजक बंधन होते हैं, लेकिन उनके इलेक्ट्रॉन वितरण सममित नहीं होते हैं। (4) H2 एक गैर-ध्रुवीय अणु है जिसमें इलेक्ट्रॉनों का सममित वितरण होता है, लेकिन हाइड्रोजन परमाणुओं के बीच का बंधन गैर-ध्रुवीय सहसंयोजक होता है
आप SAS समरूपता अभिगृहीत भुजा कोण भुजा का उपयोग करके 2 त्रिभुजों को समरूप कैसे सिद्ध कर सकते हैं?

SAS समानता प्रमेय में कहा गया है कि यदि एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हों और दोनों में सम्मिलित कोण सर्वांगसम हों, तो दोनों त्रिभुज समरूप होते हैं। एक समानता परिवर्तन एक या एक से अधिक कठोर परिवर्तन है जिसके बाद फैलाव होता है
क्या गैर-ध्रुवीय अणुओं में द्विध्रुवीय द्विध्रुवीय बल हो सकते हैं?

क्या अध्रुवीय अणु द्विध्रुव-द्विध्रुवीय बलों का प्रदर्शन कर सकते हैं? द्विध्रुव-द्विध्रुवीय बल तब उत्पन्न होते हैं जब किसी ध्रुवीय अणु का धनात्मक भाग ध्रुवीय अणु के ऋणात्मक भाग की ओर आकर्षित होता है। एक गैर-ध्रुवीय अणु में, अभी भी ध्रुवीय बंधन हो सकते हैं, यह सिर्फ इतना है कि द्विध्रुव एक दूसरे को रद्द कर देते हैं
क्या हम गैर रेखीय डेटा पर प्रतिगमन कर सकते हैं?

गैर-रेखीय प्रतिगमन कई और प्रकार के वक्रों को फिट कर सकता है, लेकिन इसके लिए सबसे अच्छा फिट खोजने और स्वतंत्र चर की भूमिका की व्याख्या करने के लिए अधिक प्रयास की आवश्यकता हो सकती है। इसके अतिरिक्त, आर-वर्ग गैर-रेखीय प्रतिगमन के लिए मान्य नहीं है, और पैरामीटर अनुमानों के लिए पी-मानों की गणना करना असंभव है
