विषयसूची:

वीडियो: त्रिभुज पर cos sin और tan क्या है?
2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
NS कोज्या (अक्सर संक्षिप्त " क्योंकि ") कोण से सटी भुजा की लंबाई और कर्ण की लंबाई का अनुपात है। और स्पर्शरेखा (अक्सर संक्षिप्त " टैन ") कोण के विपरीत पक्ष की लंबाई और आसन्न पक्ष की लंबाई का अनुपात है। SOH → पाप = "विपरीत" / "कर्ण"
इसके अलावा, आप त्रिभुज का sin cos और tan कैसे ज्ञात करते हैं?
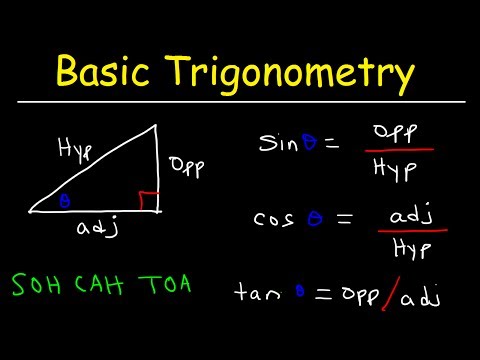
किसी भी समकोण त्रिभुज में, किसी भी कोण के लिए:
- कोण की ज्या = विपरीत भुजा की लंबाई। कर्ण की लंबाई।
- कोण की कोज्या = आसन्न भुजा की लंबाई। कर्ण की लंबाई।
- कोण की स्पर्श रेखा = विपरीत भुजा की लंबाई। आसन्न पक्ष की लंबाई।
इसके अलावा, SOH CAH TOA का सूत्र क्या है? एक समकोण त्रिभुज में लापता पक्षों और कोणों को हल करने के लिए उपयोग किए जाने वाले तीन मूल त्रिकोण अनुपातों को याद रखने में आपकी मदद करने के लिए यह एक स्मरणीय उपकरण है। इसे इस प्रकार परिभाषित किया गया है: तो ज : पाप (θ) = विपरीत / कर्ण। सीएएच : Cos(θ) = आसन्न / कर्ण।
इसके संबंध में, क्या आप किसी त्रिभुज पर सिन कॉस टैन का प्रयोग कर सकते हैं?
NS ज्या नियम कर सकते हैं में इस्तेमाल किया जा कोई त्रिभुज (सिर्फ समकोण नहीं त्रिभुज ) जहाँ एक भुजा और उसका सम्मुख कोण ज्ञात हो। आप के केवल दो भागों की जरूरत है ज्या नियम सूत्र, तीनों नहीं।
साइन कोसाइन और स्पर्शरेखा किसके लिए हैं?
यह पृष्ठ बताता है ज्या , कोज्या , स्पर्शरेखा अनुपात, उनके मूल्यों की सीमा का एक सिंहावलोकन देता है और किसी दिए गए कोण के विपरीत और आसन्न पक्षों की पहचान करने पर अभ्यास की समस्याएं प्रदान करता है। NS ज्या , कोसाइन और स्पर्शरेखा फलन एक समकोण त्रिभुज की भुजाओं के अनुपात को व्यक्त करते हैं।
सिफारिश की:
त्रिभुज ABC में लुप्त कोण माप क्या हैं?

चरण-दर-चरण स्पष्टीकरण: यह दिया गया है कि ABC एक समकोण त्रिभुज है जो C और AC = 7 इंच और CB = 5 इंच पर समकोण है। अत: त्रिभुज ABC में लुप्त कोणों की माप क्रमशः 35.5° और 54.5° है
एक 90 डिग्री कोण वाले त्रिभुज को क्या कहते हैं?

एक 90° के कोण वाले त्रिभुज को समकोण त्रिभुज कहते हैं
क्या समद्विबाहु समकोण त्रिभुज में आधार कोण हमेशा 45 मापते हैं?

एक समद्विबाहु समकोण त्रिभुज में, समान भुजाएँ समकोण बनाती हैं। ध्यान दें कि चूंकि समकोण त्रिभुज समद्विबाहु है, तो आधार पर कोण बराबर होते हैं। (प्रमेय 3.) इसलिए उन न्यून कोणों में से प्रत्येक का मान 45° है
ऐसा क्यों है कि एक अधिक त्रिभुज का लंबकेन्द्र त्रिभुज के बाहर की ओर होना चाहिए?

यह पता चला है कि तीनों ऊंचाई हमेशा एक ही बिंदु पर प्रतिच्छेद करती हैं - तथाकथित त्रिभुज का लंबकेंद्र। ऑर्थोसेंटर हमेशा त्रिभुज के अंदर नहीं होता है। यदि त्रिभुज अधिक तिरछा है, तो वह बाहर होगा। ऐसा करने के लिए ऊंचाई रेखाओं को बढ़ाया जाना चाहिए ताकि वे पार हो जाएं
आप कैसे सिद्ध करते हैं कि त्रिभुज समरूप होते हैं?

यदि त्रिभुजों के एक युग्म में संगत कोणों के दो युग्म सर्वांगसम हों, तो त्रिभुज समरूप होते हैं। हम यह जानते हैं क्योंकि यदि दो कोण जोड़े समान हैं, तो तीसरा जोड़ा भी बराबर होना चाहिए। जब तीनों कोण युग्म सभी बराबर हों, तो भुजाओं के तीनों युग्म भी समानुपात में होने चाहिए
