
वीडियो: दो बिंदुओं पर प्रतिच्छेद करने वाले वृत्तों में कितनी सामान्य आंतरिक स्पर्श रेखाएँ होती हैं?
2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
जब एक वृत्त बिना छुए दूसरे के अंदर पूरी तरह से स्थित है, कोई नहीं है सामान्य स्पर्शरेखा . कब दो वृत्त एक दूसरे को स्पर्श करें के भीतर 1 सामान्य स्पर्शरेखा के लिए खींचा जा सकता है हलकों . कब दो वृत्त दो में प्रतिच्छेद करते हैं वास्तविक और विशिष्ट अंक , 2 आम स्पर्शरेखा के लिए खींचा जा सकता है हलकों.
इसी तरह, लोग पूछते हैं कि एक बिंदु पर प्रतिच्छेद करने वाले वृत्तों में कितनी सामान्य बाह्य स्पर्श रेखाएँ होती हैं?
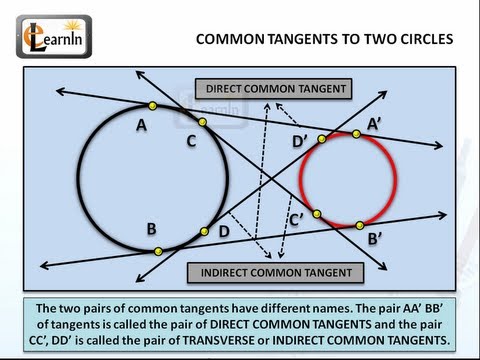
एक समतल में दो वृत्त C1 और C2 इस प्रकार दिए गए हैं कि दोनों में से कोई एक वृत्त दूसरे में समाहित नहीं है, या तो चार उभयनिष्ठ स्पर्शरेखाएँ होती हैं जब वृत्त बिल्कुल प्रतिच्छेद नहीं करते हैं या वृत्तों में तीन उभयनिष्ठ स्पर्श रेखाएँ होती हैं जब वे एक दूसरे को बाह्य रूप से स्पर्श करती हैं। या केवल दो उभयनिष्ठ स्पर्श रेखाएं जब वृत्त प्रतिच्छेद करते हैं
यह भी जानिए, क्या दो वृत्त एक ही बिंदु पर एक ही रेखा पर स्पर्शरेखा हो सकते हैं? ए स्पर्शरेखा करने के लिए वृत्त एक है रेखा ए के विमान में वृत्त जो प्रतिच्छेद करता है वृत्त ठीक एक में बिंदु . इस बिंदु कहा जाता है बिंदु स्पर्शरेखा का। दो वृत्त में वैसा ही विमान आंतरिक रूप से हैं स्पर्शरेखा यदि वे ठीक एक में प्रतिच्छेद करते हैं बिंदु और उनके अंदरूनी हिस्सों का चौराहा खाली नहीं है।
इस संबंध में, दोनों वृत्तों में उभयनिष्ठ कितनी स्पर्श रेखाएँ खींची जा सकती हैं?
तीन आम स्पर्शरेखा (एन = 3) दो बाहरी हैं स्पर्शरेखा और एक आंतरिक स्पर्शरेखा . निर्माण: खींचना बाहरी स्पर्शरेखा जैसा कि पिछले खंड में वर्णित है। आंतरिक स्पर्शरेखा इच्छा उस बिंदु से गुजरना जिसमें शामिल है दोनों मंडल तथा मर्जी के लंबवत भी हों दोनों त्रिज्या
किसी वृत्त की स्पर्श रेखा का सूत्र क्या होता है?
कैसे निर्धारित करें समीकरण का स्पर्शरेखा : निश्चित करो समीकरण का वृत्त और इसे [(x - a)^{2} + (y - b)^{2} = r^{2}] के रूप में लिखें। समीकरण , के केंद्र के निर्देशांक निर्धारित करें वृत्त ((ए; बी))। त्रिज्या का ग्रेडिएंट निर्धारित करें: [m_{CD} = frac{y_{2} - y_{1}}{x_{2}- x_{1}}]
सिफारिश की:
दो वृत्तों में कितनी उभयनिष्ठ स्पर्श रेखाएँ होती हैं?

चार आम स्पर्शरेखा
प्रतिच्छेद करने वाली रेखाओं से कौन से कोण बनते हैं?

उर्ध्वाधर कोण दो प्रतिच्छेदी रेखाओं द्वारा निर्मित कोणों के युग्म होते हैं। ऊर्ध्वाधर कोण आसन्न कोण नहीं हैं - वे एक दूसरे के विपरीत हैं। इस आरेख में, कोण a और c लंबवत कोण हैं, और कोण b और d लंबवत कोण हैं। ऊर्ध्वाधर कोण सर्वांगसम होते हैं
क्या समांतर रेखाएं तिरछी रेखाएं हैं?

त्रि-आयामी ज्यामिति में, तिरछी रेखाएँ दो रेखाएँ होती हैं जो प्रतिच्छेद नहीं करती हैं और समानांतर नहीं हैं। दो रेखाएँ जो दोनों एक ही तल में स्थित हों, या तो एक-दूसरे को पार करें या समानांतर हों, इसलिए तिरछी रेखाएँ केवल तीन या अधिक आयामों में मौजूद हो सकती हैं। दो रेखाएँ तिरछी होती हैं यदि और केवल यदि वे समतलीय न हों
उच्चतम द्रव्यमान संख्या वाले सिलिकन के परमाणु में प्रोटॉनों की संख्या कितनी होती है?

उदाहरण के लिए, सिलिकॉन में 14 प्रोटॉन और 14 न्यूट्रॉन होते हैं। इसका परमाणु क्रमांक 14 है और इसका परमाणु द्रव्यमान 28 है। यूरेनियम के सबसे सामान्य समस्थानिक में 92 प्रोटॉन और 146 न्यूट्रॉन हैं। इसका परमाणु क्रमांक 92 है और इसका परमाणु द्रव्यमान 238 (92 + 146) है। 2.1 इलेक्ट्रॉन, प्रोटॉन, न्यूट्रॉन और परमाणु। तत्व लौह प्रतीक Fe प्रत्येक कोश में इलेक्ट्रॉनों की संख्या प्रथम 2 द्वितीय 8 तृतीय 14
क्या समांतर रेखाएं अतिपरवलयिक ज्यामिति में प्रतिच्छेद करती हैं?

अतिपरवलयिक ज्यामिति में दो प्रकार की समानांतर रेखाएँ होती हैं। यदि दो रेखाएँ अतिपरवलयिक ज्यामिति के एक मॉडल के भीतर प्रतिच्छेद नहीं करती हैं, लेकिन वे इसकी सीमा पर प्रतिच्छेद करती हैं, तो रेखाएँ स्पर्शोन्मुख रूप से समानांतर या अतिपरवलयिक कहलाती हैं।
