विषयसूची:

वीडियो: गाऊसी उन्मूलन का उपयोग करके आप एक रैखिक समीकरण को कैसे हल करते हैं?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
समीकरणों के सिस्टम को हल करने के लिए गॉसियन एलिमिनेशन का उपयोग कैसे करें
- आप किसी भी पंक्ति को गुणा कर सकते हैं द्वारा एक स्थिरांक (शून्य के अलावा)। पंक्ति तीन को गुणा करता है द्वारा -2 आपको एक नई पंक्ति तीन देने के लिए।
- आप किन्हीं दो पंक्तियों को स्विच कर सकते हैं। एक और दो पंक्तियों को स्वैप करें।
- आप दो पंक्तियों को एक साथ जोड़ सकते हैं। एक और दो पंक्तियों को जोड़ता है और लिखता है में पंक्ति दो।
फिर, गाऊसी उन्मूलन कैसे कार्य करता है?
शिथिल बोल, गाऊसी उन्मूलन कार्य ऊपर से नीचे तक, सोपानक रूप में एक मैट्रिक्स का निर्माण करने के लिए, जबकि गॉस -जॉर्डन निकाल देना कहाँ जारी है गाऊसी तब तक छोड़ दिया गया था जब तक कि नीचे से ऊपर की ओर काम करते हुए कम किए गए सोपानक रूप में एक मैट्रिक्स का निर्माण किया गया था। तकनीक को निम्नलिखित उदाहरण में चित्रित किया जाएगा।
इसके अलावा, क्रैमर का नियम मैट्रिक्स क्या है? क्रैमर का नियम 2×2 प्रणाली के लिए (दो चर के साथ) क्रैमर का नियम एक अन्य विधि है जो निर्धारकों का उपयोग करके रैखिक समीकरणों की प्रणालियों को हल कर सकती है। नोटेशन के संदर्भ में, a आव्यूह वर्ग कोष्ठकों द्वारा संलग्न संख्याओं की एक सरणी है, जबकि सिद्ध दो लंबवत सलाखों से घिरी संख्याओं की एक सरणी है।
दूसरे, गाऊसी उन्मूलन का उद्देश्य क्या है?
गाउस विलोपन . विकिपीडिया, मुक्त विश्वकोश से। गाउस विलोपन पंक्ति में कमी के रूप में भी जाना जाता है, रैखिक समीकरणों की एक प्रणाली को हल करने के लिए रैखिक बीजगणित में एक एल्गोरिथ्म है। इसे आमतौर पर गुणांक के संबंधित मैट्रिक्स पर किए गए संचालन के अनुक्रम के रूप में समझा जाता है।
गॉसियन और गॉस जॉर्डन के उन्मूलन में क्या अंतर है?
3 उत्तर। गाउस विलोपन एक मैट्रिक्स को पंक्ति सोपानक रूप में रखने में मदद करता है, जबकि गॉस - जॉर्डन उन्मूलन मैट्रिक्स को कम पंक्ति के सोपानक रूप में रखता है। छोटी प्रणालियों (या हाथ से) के लिए, आमतौर पर इसका उपयोग करना अधिक सुविधाजनक होता है गॉस - जॉर्डन उन्मूलन और प्रतिनिधित्व किए गए प्रत्येक चर के लिए स्पष्ट रूप से हल करें में मैट्रिक्स प्रणाली।
सिफारिश की:
आप अशक्त कारक नियम का उपयोग करके द्विघात समीकरण को कैसे हल करते हैं?

इससे हम यह निष्कर्ष निकाल सकते हैं कि: यदि किन्हीं दो संख्याओं का गुणनफल शून्य है, तो एक या दोनों संख्याएँ शून्य हैं। अर्थात्, यदि ab = 0, तो a = 0 या b = 0 (जिसमें संभावना है कि a = b = 0) शामिल है। इसे नल कारक नियम कहा जाता है; और हम इसका उपयोग अक्सर द्विघात समीकरणों को हल करने के लिए करते हैं
डेसकार्टेस के संकेतों के नियम का उपयोग करके आप काल्पनिक मूल कैसे प्राप्त करते हैं?

डेसकार्टेस के संकेतों का नियम कहता है कि सकारात्मक जड़ों की संख्या f (x) के संकेत में परिवर्तन के बराबर है, या एक सम संख्या से कम है (इसलिए आप 2 को तब तक घटाते रहते हैं जब तक कि आपको 1 या 0 प्राप्त न हो जाए)। इसलिए, पिछले f(x) के 2 या 0 धनात्मक मूल हो सकते हैं। नकारात्मक वास्तविक जड़ें
अनुभवजन्य नियम का उपयोग करके आप अनुमानित प्रतिशत कैसे ज्ञात करते हैं?

वक्र के नीचे का क्षेत्रफल x = 9 से x = 13 तक ज्ञात करना। अनुभवजन्य नियम या 68-95-99.7% नियम डेटा का अनुमानित प्रतिशत देता है जो एक मानक विचलन (68%), दो मानक विचलन (95%) के अंतर्गत आता है। , और माध्य के तीन मानक विचलन (99.7%)
आप एक रैखिक असमानता समीकरण को कैसे हल करते हैं?

तीन चरण हैं: समीकरण को पुनर्व्यवस्थित करें ताकि 'y' बाईं ओर हो और बाकी सब दाईं ओर। 'y=' रेखा को आलेखित करें (इसे y≤ या y≥ के लिए एक ठोस रेखा बनाएं, और y के लिए एक धराशायी रेखा बनाएं) रेखा के ऊपर 'से अधिक' (y> या y≥) के लिए या रेखा के नीचे छायांकित करें। 'से कम' (y< या y≤)
आप चर को अलग करके समीकरण को कैसे हल करते हैं?
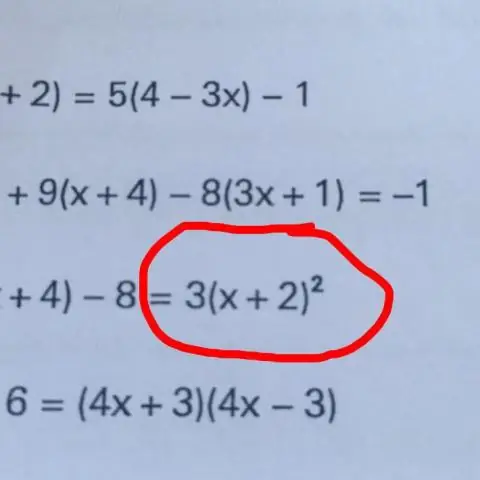
एक चर को अलग करने की मूल तकनीक समीकरण के "दोनों पक्षों के लिए कुछ करना" है, जैसे समीकरण के दोनों पक्षों को एक ही संख्या से जोड़ना, घटाना, गुणा करना या विभाजित करना। इस प्रक्रिया को दोहराकर, हम समीकरण के एक तरफ चर को पृथक कर सकते हैं
