
वीडियो: आप एक पैरामीट्रिक समीकरण का उन्मुखीकरण कैसे पाते हैं?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
NS दिशा विमान का वक्र के रूप में पैरामीटर वृद्धि को कहा जाता है अभिविन्यास का वक्र . NS अभिविन्यास विमान का वक्र के साथ खींचे गए तीरों द्वारा दर्शाया जा सकता है वक्र . नीचे दिए गए ग्राफ की जांच करें। इसे द्वारा परिभाषित किया गया है पैरामीट्रिक समीकरण x = cos(t), y = sin(t), 0≦t < 2Π।
यहाँ, आप ग्राफ़ के अभिविन्यास को कैसे जानते हैं?
प्रत्येक ग्राफ एक चक्रीय है अभिविन्यास ; सभी चक्रीय झुकाव शीर्षों को एक क्रम में रखकर प्राप्त किया जा सकता है, और फिर प्रत्येक किनारे को उसके पहले के अंतिम बिंदुओं से अनुक्रम में बाद के समापन बिंदु तक निर्देशित किया जा सकता है।
इसके अतिरिक्त, एक पैरामीटरकरण क्या है? गणित में, और विशेष रूप से ज्यामिति में, पैरामीट्रिजेशन (या मानकीकरण ; भी मानकीकरण , parametrisation) एक अंतर्निहित समीकरण द्वारा परिभाषित एक वक्र, एक सतह, या अधिक सामान्यतः, कई गुना या विविधता के पैरामीट्रिक समीकरणों को खोजने की प्रक्रिया है।
फिर, पैरामीट्रिक ग्राफ क्या है?
तो, ए पैरामीट्रिक एक तीसरे चर के तहत वक्र के निर्देशांक और -निर्देशांक के लिए दो अलग-अलग कार्यों के तहत वक्र को परिभाषित किया गया है, जिसे एक पैरामीटर कहा जाता है। अक्सर पैरामीटर "" का उपयोग किया जाता है और अक्सर "समय" का प्रतिनिधित्व करने के लिए प्रतीकात्मक रूप से उपयोग किया जाता है क्योंकि एक कण एक वक्र को पार करता है।
वेक्टर समीकरण क्या है?
वेक्टर समीकरण एक सीधी रेखा का कार्टेशियन समीकरण एक सीधी रेखा के लिए y = mx + c है, जहाँ m रेखा की प्रवणता का प्रतिनिधित्व करता है, और c वह बिंदु है जहाँ रेखा y-अक्ष को पार करती है। ए वेक्टर समीकरण एक रेखा के लिए समान रूप से 2 जानकारी की आवश्यकता होती है: रेखा पर एक बिंदु। रेखा की दिशा।
सिफारिश की:
आप क्षैतिज खिंचाव कैसे पाते हैं?

यदि b>1, ग्राफ y-अक्ष के सापेक्ष या लंबवत रूप से फैला है। यदि b<1, ग्राफ y-अक्ष के सापेक्ष सिकुड़ता है। सामान्य तौर पर, समीकरण y=f(cx) y = f (c x) द्वारा एक क्षैतिज खिंचाव दिया जाता है
पैरामीट्रिक समीकरणों का उपयोग क्यों किया जाता है?
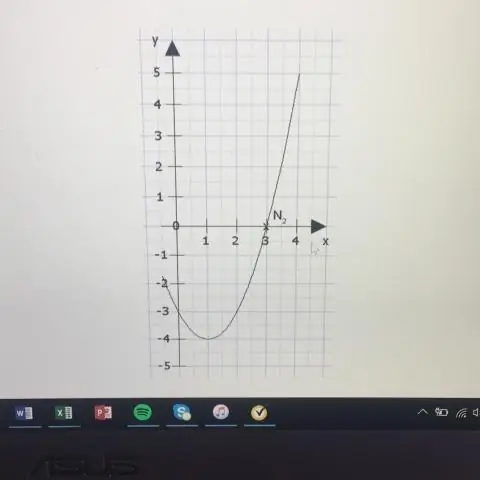
पैरामीट्रिक समीकरणों के फायदों में से एक यह है कि उनका उपयोग उन वक्रों को ग्राफ़ करने के लिए किया जा सकता है जो कार्य नहीं हैं, जैसे कि यूनिट सर्कल। पैरामीट्रिक समीकरणों का एक अन्य लाभ यह है कि पैरामीटर का उपयोग किसी उपयोगी चीज़ का प्रतिनिधित्व करने के लिए किया जा सकता है और इसलिए हमें ग्राफ़ के बारे में अतिरिक्त जानकारी प्रदान करता है
आप कैसे बता सकते हैं कि दो समीकरण समानांतर हैं?

हम उनके समीकरणों से यह निर्धारित कर सकते हैं कि क्या दो रेखाएँ उनके ढलानों की तुलना करके समानांतर हैं। यदि ढलान समान हैं और y-अवरोधन भिन्न हैं, तो रेखाएँ समानांतर होती हैं। यदि ढलान अलग हैं, तो रेखाएं समानांतर नहीं हैं। समानांतर रेखाओं के विपरीत, लंबवत रेखाएं प्रतिच्छेद करती हैं
आप एक लघुगणकीय समीकरण का स्पर्शोन्मुख कैसे पाते हैं?

मुख्य बिंदु जब रेखांकन किया जाता है, तो लॉगरिदमिक फ़ंक्शन वर्गमूल फ़ंक्शन के आकार में समान होता है, लेकिन एक लंबवत स्पर्शोन्मुख के साथ x दाईं ओर से 0 की ओर बढ़ता है। बिंदु (1,0) y=logbx y = l o g b x के रूप के सभी लघुगणकीय कार्यों के ग्राफ पर है, जहां b एक सकारात्मक वास्तविक संख्या है
2 रास्ता अनोवा पैरामीट्रिक या गैर-पैरामीट्रिक है?

क्या दोतरफा एनोवा के बराबर गैर-पैरामीट्रिक है? साधारण टू-वे एनोवा सामान्य डेटा पर आधारित है। जब डेटा क्रमिक होता है तो किसी को दो तरह के एनोवा के गैर-पैरामीट्रिक समकक्ष की आवश्यकता होती है
