
वीडियो: आप एक क्षैतिज परवलय का शीर्ष कैसे ज्ञात करते हैं?
2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
यदि एक परवलय एक क्षैतिज अक्ष, के समीकरण का मानक रूप परवलय क्या यह है: (y-k)2 = 4p(x - h), जहाँ p≠ 0. The शिखर इस का परवलय (एच, के) पर है। फोकस (h + p, k) पर है। डायरेक्ट्रिक्स लाइन x = h - p है।
बस इतना ही, आप एक परवलय का शीर्ष और नियतांक कैसे ज्ञात करते हैं?
मानक रूप है (x - h)2 = 4p (y - k), जहाँ केंद्र है (एच, के + पी) और नियता वाई = के - पी है। अगर परवलय घुमाया जाता है ताकि उसका शिखर है (एच, के) और इसकी सममिति की धुरी एक्स-अक्ष के समानांतर है, इसमें एक है समीकरण का (वाई - के)2 = 4p (x -h), जहां केंद्र है (एच + पी, के) और नियता एक्स = एच - पी है।
इसके अतिरिक्त, एक बग़ल में परवलय के लिए समीकरण क्या है? A. का "सामान्य" रूप परवलय का समीकरण वह है जिसका आप अभ्यस्त हैं, y = ax2 + बीएक्स + सी - जब तक कि द्विघात " बग़ल में ", किस मामले में समीकरण कुछ इस तरह दिखेगा x = ay2 + द्वारा + सी।
बस इतना ही, आप एक परवलय समीकरण का शीर्ष कैसे ज्ञात करते हैं?
यह बिंदु, जहां परवलय दिशा बदलता है, कहा जाता है " शिखर ". यदि द्विघात को y = a(x - h) के रूप में लिखा जाता है2 + के, फिर शिखर बिंदु (एच, के) है। यह समझ में आता है, अगर आप इसके बारे में सोचते हैं। वर्गाकार भाग हमेशा धनात्मक होता है (दाईं ओर-ऊपर के लिए परवलय ), जब तक कि यह शून्य न हो।
परवलय का शीर्ष p के किस मान के लिए है?
पूर्ण p. का मान के बीच की दूरी है शिखर और फोकस और के बीच की दूरी शिखर और डायरेक्टिक्स। (साइन ऑन पी मुझे किस तरह से बताता है परवलय फलक।) चूँकि फोकस और डायरेक्ट्रिक्स दो इकाई अलग हैं, तो यह दूरी एक इकाई होनी चाहिए, इसलिए | पी | = 1.
सिफारिश की:
आप कैसे निर्धारित करते हैं कि किसी फ़ंक्शन में क्षैतिज स्पर्शरेखा रेखा है या नहीं?

क्षैतिज रेखाओं का ढलान शून्य होता है। इसलिए, जब अवकलज शून्य होता है, तो स्पर्श रेखा क्षैतिज होती है। क्षैतिज स्पर्शरेखा रेखाओं को खोजने के लिए, शून्य का पता लगाने के लिए फ़ंक्शन के व्युत्पन्न का उपयोग करें और उन्हें मूल समीकरण में वापस प्लग करें
आप मानक शीर्ष को गुणनखंडित रूप में कैसे परिवर्तित करते हैं?

द्विघात के विभिन्न रूपों के बीच रूपांतरण - Expii. मानक रूप ax^2 + bx + c है। शीर्ष रूप a(x-h)^2 + k है, जो समरूपता के शीर्ष और अक्ष को प्रकट करता है। गुणनखंडित रूप a(x-r)(x-s) है, जो जड़ों को प्रकट करता है
आप शीर्ष पर पिरामिड के साथ घन का आयतन कैसे ज्ञात करते हैं?
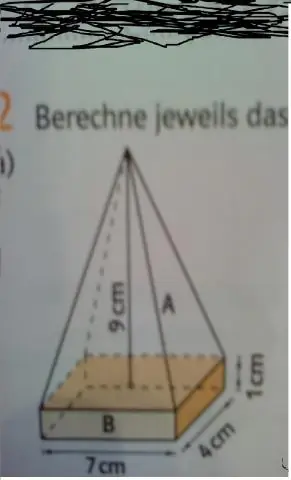
इस घन का आयतन ज्ञात करने के लिए, आधार गुणा चौड़ाई गुणा ऊंचाई गुणा करें। पिरामिड का आयतन ज्ञात करने के लिए, आधार का क्षेत्रफल लें, egin{align*}Bend{align*} और इसे ऊँचाई से गुणा करें और फिर इसे egin{align*}frac{1}{3}end{ से गुणा करें। संरेखित करें*}
आप समरूपता के शीर्ष और अक्ष को कैसे लेबल करते हैं?
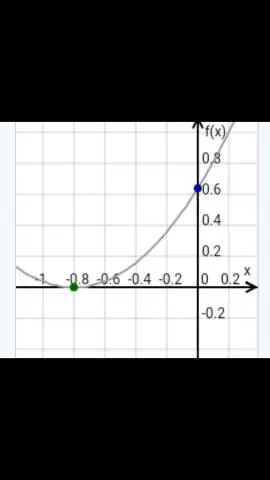
समरूपता की धुरी हमेशा परवलय के शीर्ष से होकर गुजरती है। शीर्ष का x-निर्देशांक परवलय की सममिति के अक्ष का समीकरण है। मानक रूप में द्विघात फलन के लिए, y=ax2+bx+c, सममिति की धुरी एक ऊर्ध्वाधर रेखा है x=−b2a
आप क्षैतिज अनंतस्पर्शी कैसे रेखांकन करते हैं?

यदि अंश की डिग्री हर की डिग्री के बराबर है, तो क्षैतिज अनंतस्पर्शी गुणांक के अनुपात द्वारा उच्चतम डिग्री शर्तों पर दिया जाता है। यदि अंश की डिग्री हर की डिग्री से कम है, तो क्षैतिज अनंतस्पर्शी x-अक्ष है, या रेखा y=0
