
वीडियो: द्विघात समीकरण में B क्या है?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
द्विघात समारोह: द्विघात फलन f(x) = a * x^2 + बी * x + c, जो आपको बताता है कि फंक्शन रेखांकन जैसा दिखेगा। बी -मूल्य: The बी -मान मध्य संख्या है, जो x के आगे और गुणा की गई संख्या है; के मूल्य में परिवर्तन बी परवलय और परिणामी ग्राफ को प्रभावित करता है।
यहाँ, द्विघात सूत्र में B क्या है?
NS द्विघात सूत्र "ए", "का उपयोग करता है बी ", और" c "से" ax2 + बीएक्स + सी", जहां "ए", " बी ", और"सी" केवल संख्याएं हैं; वे "संख्यात्मक गुणांक" हैं द्विघात समीकरण उन्होंने आपको हल करने के लिए दिया है।
दूसरे, द्विघात समीकरण में A क्या है? बीजगणित में, a द्विघात समीकरण (लैटिनक्वाड्रैटस से "वर्ग" के लिए) कोई भी है समीकरण फॉर्म होना। जहां एक्स अज्ञात का प्रतिनिधित्व करता है, और ए, बी, और सी ≠ 0 के साथ ज्ञात संख्याओं का प्रतिनिधित्व करते हैं। यदि ए = 0, तो समीकरण रेखीय, नहीं द्विघात , क्योंकि कोई पद नहीं है।
इसके अलावा, एक परवलय के समीकरण में B क्या है?
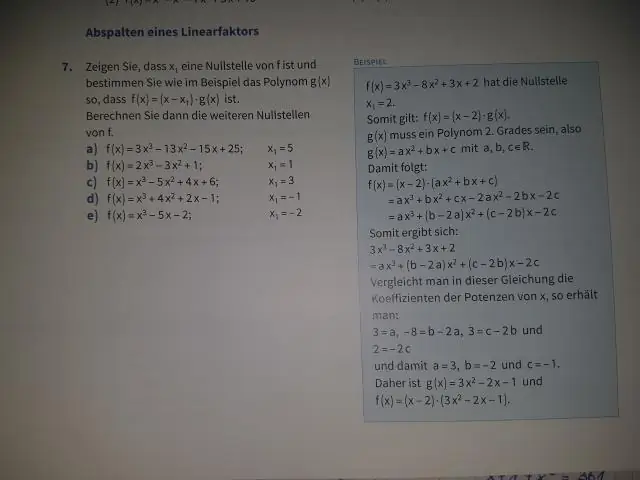
मानक परवलय का समीकरण is.y=ax2+ बी एक्स + सी। लेकिन वो समीकरण एक के लिए परवलय "वर्टेक्स फॉर्म" में भी लिखा जा सकता है: y=a(x−h)2+k। इसमें समीकरण , का शीर्ष परवलय बिंदु (एच, के) है।
द्विघात फलन के 3 रूप क्या हैं?
जबकि लिखने के अधिकांश तरीके द्विघात समीकरण बेमानी और बेकार हैं, वहाँ हैं तीन रूप जिसका वास्तव में अद्वितीय उपयोग है। इन तीन मुख्य फार्म जिससे हम परवलय का रेखांकन करते हैं, मानक कहलाते हैं प्रपत्र , अवरोधन प्रपत्र और शीर्ष प्रपत्र.
सिफारिश की:
आप अशक्त कारक नियम का उपयोग करके द्विघात समीकरण को कैसे हल करते हैं?

इससे हम यह निष्कर्ष निकाल सकते हैं कि: यदि किन्हीं दो संख्याओं का गुणनफल शून्य है, तो एक या दोनों संख्याएँ शून्य हैं। अर्थात्, यदि ab = 0, तो a = 0 या b = 0 (जिसमें संभावना है कि a = b = 0) शामिल है। इसे नल कारक नियम कहा जाता है; और हम इसका उपयोग अक्सर द्विघात समीकरणों को हल करने के लिए करते हैं
द्विघात बहुपद को द्विघात क्यों कहा जाता है?
ऐसा इसलिए है क्योंकि वर्ग के लिए क्वाड्राटम लैटिन शब्द है, और चूँकि x की भुजा की लंबाई वाले वर्ग का क्षेत्रफल x2 द्वारा दिया जाता है, एक बहुपद समीकरण जिसमें घातांक दो होते हैं, द्विघात ('वर्ग-समान') समीकरण के रूप में जाना जाता है। विस्तार से, एक द्विघात सतह एक दूसरे क्रम का बीजीय सतह है
आप C++ में द्विघात समीकरण कैसे लिखते हैं?
प्रोग्राम 2: द्विघात समीकरण में a b और c खोजें #include #include int main(){float a,b,c; फ्लोट डी, रूट 1, रूट 2; प्रिंटफ ('x^2+bx+c:' प्रारूप में द्विघात समीकरण दर्ज करें); स्कैनफ ('%fx^2%fx%f',&a,&b,&c); डी = बी * बी - 4 * ए * सी;
आप द्विघात समीकरण को शीर्ष रूप से कैलकुलेटर में कैसे बदलते हैं?

मूल रूप से शीर्ष रूप में रूपांतरण के लिए कैलकुलेटर y=x2+3x+5. x2+3x+5= || +(p2)2-(p2)2=0. || a2+2ab+b2=(a+b)2. || -1⋅-1 = +1। एक्सएस=-32=-1.5. वाईएस=-(32)2+5=2.75
आप एक द्विघात समीकरण को सामान्य रूप से मानक रूप में कैसे बदलते हैं?

कोई भी द्विघात फलन मानक रूप f(x) = a(x - h) 2 + k में लिखा जा सकता है जहाँ h और k गुणांक a, b और c के रूप में दिए गए हैं। आइए हम सामान्य रूप में द्विघात फलन से शुरू करें और मानक रूप में इसे फिर से लिखने के लिए वर्ग को पूरा करें
