
वीडियो: परवलय में डायरेक्ट्रिक्स क्या है?

2024 लेखक: Miles Stephen | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:36
नियता . ए परवलय एक समतल में सभी बिंदुओं का समुच्चय होता है जो किसी दिए गए बिंदु और दी गई रेखा से समान दूरी पर होते हैं। बिंदु को का फोकस कहा जाता है परवलय , और रेखा को कहा जाता है नियता . NS नियता a. की सममिति के अक्ष के लंबवत है परवलय और स्पर्श नहीं करता परवलय.
इसके अलावा, आप एक परवलय का डायरेक्ट्रिक्स कैसे खोजते हैं?
मानक रूप है (x - h)2 = 4p (y - k), जहां फोकस (h, k + p) है और नियता वाई = के - पी है। अगर परवलय घुमाया जाता है ताकि इसका शीर्ष (h, k) हो और इसकी सममिति की धुरी x-अक्ष के समानांतर हो, इसमें (y - k) का समीकरण होता है2 = 4p (x - h), जहां फोकस (h + p, k) है और नियता एक्स = एच - पी है।
साथ ही, आप परवलय का शीर्ष रूप कैसे ज्ञात करते हैं? एफ (एक्स) = ए (एक्स - एच)2 + के, जहां (एच, के) है शिखर का परवलय . FYI करें: विभिन्न पाठ्यपुस्तकों में "मानक" संदर्भ की अलग-अलग व्याख्याएँ हैं प्रपत्र "एक द्विघात फलन का। कुछ लोग कहते हैं f (x) = ax2 + बीएक्स + सी "मानक" है प्रपत्र ", जबकि अन्य कहते हैं कि f (x) = a(x - h)2 + k "मानक" है प्रपत्र ".
इसी प्रकार कोई भी पूछ सकता है कि अतिपरवलय का निदेश क्या है?
ए के मामले में अतिशयोक्ति , ए नियता एक सीधी रेखा है जहाँ पर प्रत्येक बिंदु से दूरी अतिशयोक्ति इसके दो फोकस में से एक के लिए लंबवत दूरी से गुणा है नियता , जहां से एक स्थिरांक अधिक है। ध्यान दें कि अतिपरवलय प्रत्येक फोकस के लिए दो फोकस और दो निर्देश हैं।
आप किसी समीकरण का निदेश कैसे ज्ञात करते हैं?
मानक रूप है (x - h)2 = 4p (y - k), जहां फोकस (h, k + p) है और नियता वाई = के - पी है। यदि परवलय को इस प्रकार घुमाया जाता है कि इसका शीर्ष (h, k) हो और इसकी सममिति की धुरी x-अक्ष के समानांतर हो, तो इसका एक समीकरण का (वाई - के)2 = 4p (x - h), जहां फोकस (h + p, k) है और नियता एक्स = एच - पी है।
सिफारिश की:
आप शीर्ष और डायरेक्ट्रिक्स कैसे खोजते हैं?

मानक रूप है (x - h)2 = 4p (y - k), जहां फोकस (h, k + p) है और डायरेक्ट्रिक्स y = k - p है। यदि परवलय को इस प्रकार घुमाया जाता है कि इसका शीर्ष (h,k) है और इसकी सममिति की धुरी x-अक्ष के समानांतर है, तो इसका समीकरण (y-k)2 = 4p (x-h) होता है, जहां फोकस है (h + p, k) और नियतांक x = h - p . है
क्या सेंट लुइस आर्क एक परवलय है?

इस लेख ने दिखाया है कि गेटवे आर्क एक परवलय नहीं है। बल्कि, यह एक चपटा (या भारित) कैटेनरी के आकार में होता है, जो कि दो निश्चित बिंदुओं के बीच में पतली श्रृंखला को लटकाने पर हमें दिखाई देने वाली आकृति है।
आप परवलय के एक शंकु का आलेख कैसे बनाते हैं?
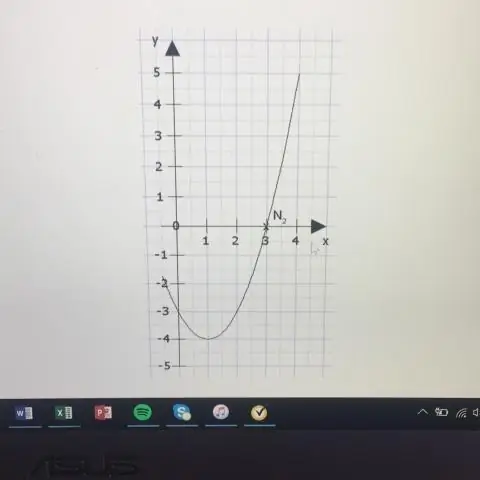
दिशा रेखा y = k - p है। अक्ष रेखा x = h है। यदि p>0, परवलय ऊपर की ओर खुलता है, और यदि p<0, तो परवलय नीचे की ओर खुलता है। यदि एक परवलय का एक क्षैतिज अक्ष है, तो परवलय के समीकरण का मानक रूप यह है: (y - k)2 = 4p(x - h), जहाँ p≠ 0
आप एक क्षैतिज परवलय का शीर्ष कैसे ज्ञात करते हैं?

यदि परवलय का एक क्षैतिज अक्ष है, तो परवलय के समीकरण का मानक रूप यह है: (y -k)2 = 4p(x - h), जहाँ p≠ 0. इस परवलय का शीर्ष (h, k) पर है। फोकस (h + p, k) पर है। दिशा रेखा x = h - p . है
आप परवलय का एक शंकु खंड कैसे बनाते हैं?
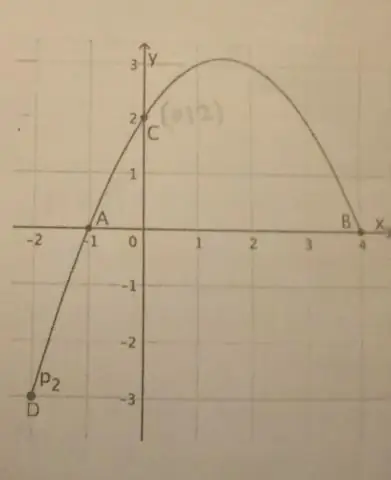
यदि एक परवलय का एक ऊर्ध्वाधर अक्ष है, तो परवलय के समीकरण का मानक रूप यह है: (x - h)2 = 4p(y - k), जहाँ p≠ 0. इस परवलय का शीर्ष (h, k) पर है। फोकस (h, k + p) पर है। दिशा रेखा y = k - p . है
